19/12/2024 19:15

Công thức tính thể tích hình chóp cụt, diện tích xung quanh và toàn phần của hình chóp cụt

Cùng tìm hiểu hình chóp cụt là gì, cách tính thể tích hình chóp cụt, diện tích xung quanh và toàn phần của hình chóp cụt trong bài viết dưới đây nhé.

Định nghĩa hình chóp cụt

Hình chóp cụt là một phần của khối đa diện, nằm giữa mặt đáy và thiết diện cắt bởi mặt phẳng song song với đáy của hình chóp.

Hình gồm các đa giác A1A2...An,B1B2...BnA1A2...An,B1B2...Bn và các hình thang A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn được gọi là một hình chóp cụt, kí hiệu là A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
Một cách đơn giản, hình chóp cụt được tạo thành từ hình chóp S.A1A2...AnS.A1A2...An sau khi cắt đi hình chóp S.B1B2...Bn.S.B1B2...Bn.

+ Các đa giác A1A2...An,B1B2...BnA1A2...An,B1B2...Bn được gọi là hai mặt đáy,

+ Các hình thang A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn được gọi là các mặt bên.

+ Các đoạn thẳng A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn được gọi là các cạnh bên, các cạnh của mặt đáy được gọi là các cạnh đáy.

+ Khoảng cách giữa hai mặt đáy được gọi là chiều cao của hình chóp cụt.

Tính chất của hình chóp cụt:

Hai đáy là hai đa giác (hình tam giác, tứ giác, ngũ giác,…) có các cạnh tương ứng song song và tỉ số các cạnh tương ứng bằng nhau.
Các mặt bên đều là những hình thang.
Các đường thẳng chứa các cạnh bên sẽ đồng quy tại một điểm (đỉnh của hình chóp)
Hình chóp cụt đều là hình chóp cụt có các mặt đáy là hình đa giác đều (có các cạnh bằng nhau). Do đó, các mặt bên của hình chóp cụt đều là những hình thang cân bằng nhau.

Công thức tính diện tích hình chóp cụt

Công thức tính thể tích hình chóp cụt, diện tích xung quanh và toàn phần của hình chóp cụt

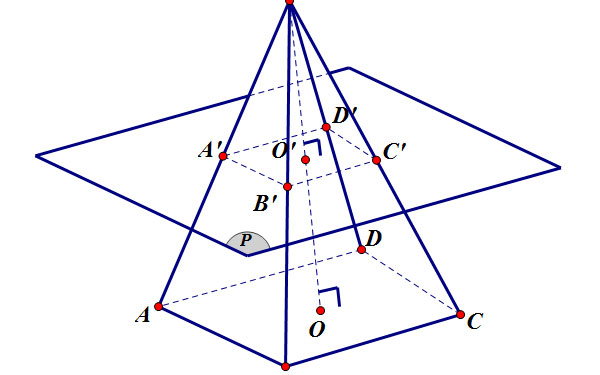
Diện tích xung quanh hình chóp cụt

Diện tích xung quanh hình chóp cụt là diện tích của các mặt xung quanh, phần bao quanh hình chóp cụt, không gồm diện tích hai đáy.

Cách tính diện tích xung quanh của hình chóp cụt: Tính diện tích từng mặt bên (các hình thang) của hình chóp cụt theo công thức tính diện tích hình thang bình thường, sau đó tính tổng diện tích.

Công thức tính diện tích hình chóp cụt đều:

Trong đó:

Sxq: diện tích xung quanh
n: số lượng mặt bên của hình chóp cụt (bằng số cạnh của đa giác đáy)
a, b: chiều dài cạnh của lần lượt 2 đáy trên và dưới
h: chiều cao của các tứ giác mặt bên.

Ví dụ 1:

Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng 10cm và 15cm, chiều cao của mặt bên bằng 12cm.

Giải:

Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên là:

$\frac{\left(10+15\right)\times12}{2}=150\ \left(cm^2\right)$

Hình chóp cụt tứ giác đều có 4 mặt bên bằng nhau nên diện tích xung quanh bằng:

150 x 4 = 600 (cm2)

Ví dụ 2: Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng 6cm và 8cm, chiều cao của mặt bên bằng 5cm.Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng 6cm và 8cm.

Giải:

Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên bằng

$\frac{\left(6+8\right)\times5}{2}=35\ \left(cm^2\right)$

Hình chóp cụt tứ giác đều có 4 mặt bên bằng nhau nên diện tích xung quanh bằng

35 x 4 = 140 (cm2)

Diện tích toàn phần của hình chóp cụt

Diện tích toàn phần của hình chóp cụt bằng tổng diện tích xung quanh và diện tích 2 mặt đáy

Công thức: Stp = Sxq + Sđáy lớn + Sđáy nhỏ

Trong đó:

Stp: Diện tích toàn phần
Sxq: Diện tích xung quanh
Sđáy lớn: Diện tích đáy lớn
Sđáy nhỏ: Diện tích đáy nhỏ

Ví dụ:

Tính diện tích toàn phần của hình chóp cụt đều theo các kích thước cho trên hình.

Giải:

Ta có: $A_1D_1\ =\ 6\ =>\ O_1I\ =3$

AD = 12 ⇒ OJ = 6

Kẻ II1 ⊥ OJ ta có: I1J = 3

Áp dụng định lí pi-ta-go vào tam giác vuông II1J ta có:

IJ2 = II12 + I1J2 = 92 + 32 = 90

Suy ra: $IJ\ =\ \sqrt{90}$

Diện tích mặt một bên là một hình thang bằng:

$S=\frac{\left(6+12\right)}{2}\ \times\sqrt{90}=9\sqrt{90}(đvdt)$

Diện tích xung quanh bằng: $Sxq=4\times9\times\sqrt{9}0=36\sqrt{9}0(đvdt)$

Diện tích đáy trên bằng: S = 6 x 6 = 36(đvdt)

Diện tích đáy dưới bằng: S= 12 x 12 =144 (đvdt)

Diện tích toàn phần của hình chóp cụt bằng:

$S_{tp}=36\sqrt{90}+36+144=(36\sqrt{90}+180)\ (đvdt)$

Công thức tính thể tích hình chóp cụt

Công thức:

Trong đó:

V: thể tích hình chóp cụt
S, S’ lần lượt là diện tích mặt đáy lớn và đáy nhỏ của hình chóp chụt
h: chiều cao của hình chóp, tức là khoảng cách giữa 2 mặt đáy lớn và đáy nhỏ

Hình chóp cụt có là hình vuông (tứ giác đều):

Trong đó:

V: Thể tích
h: Chiều cao của hình chóp
a, b lần lượt là chiều dài cạnh của mặt đáy lớn và đáy nhỏ

Link nội dung: https://suckhoegd.com/cong-thuc-tinh-the-tich-hinh-chop-cut-dien-tich-xung-quanh-va-toan-phan-cua-hinh-chop-cut-a14892.html