Công thức tính đường chéo hình lập phương là công thức khá phổ biến nhưng để áp dụng trong bài tập thì bạn cần có phương pháp cụ thể. Hãy cùng Clevai tìm hiểu các dạng bài liên quan qua bài viết dưới đây nhé!
Nếu bạn đang quan tâm đến các bài toán liên quan đến đường chéo hình lập phương thì không nên bỏ qua bài viết dưới đây của Clevai. Bài viết này sẽ hướng dẫn bạn cách giải bài tập, áp dụng các công thức tính nhanh nhất và chính xác nhất.
1. Đường chéo hình lập phương là gì?
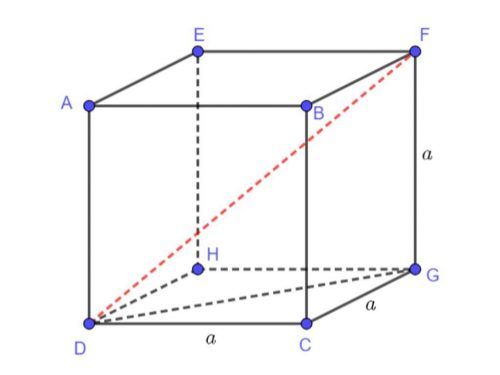
Trước khi bạn muốn tìm hiểu đường chéo hình lập phương là gì? Bạn cần tìm hiểu về định nghĩa hình lập phương trước. Hình lập phương là khối hình có tất cả 8 đỉnh và 6 mặt đều là hình vuông bằng nhau, gồm 12 cạnh có chiều dài bằng nhau. Hình lập phương có 4 đường chéo được cắt nhau tại 1 điểm và điểm đó được xem là tâm đối xứng hình lập phương. Đường chéo mặt bên và đường chéo hình khối lập phương dài bằng nhau.
2. Công thức tính đường chéo hình lập phương
Khi xét hình lập phương ABCD.A'B'C’D' có cạnh a. Áp dụng định lý Pitago bạn sẽ tính được:
- Đường chéo của 1 mặt AC = a√2
- Đường chéo của hình lập phương AC' = √(AC2 + CC'2) = √(2a2 + a2) = a√3
Về công thức tính đường chéo của hình lập phương sẽ có 2 công thức tính độ dài phổ biến đó là:
- Công thức tính độ dài đường chéo hình lập phương: D = a√3
- Công thức tính độ dài đường chéo mặt bên hình lập phương: d = a√2
Trong đó:
a là độ dài cạnh
D là đường chéo của hình lập phương
d là đường chéo mặt bên
Đối với một số bài toán ngoài câu hỏi tìm độ dài đường chéo của hình lập phương. Yêu cầu đề bài còn cần tìm thể tích của hình lập phương đó. Vậy nên, bạn cũng cần phải nắm được công thức tính thể tích hình lập phương đó là:
V= a3
3. Hướng dẫn giải bài tập đường chéo hình lập phương
Có khá nhiều dạng bài tập áp dụng công thức tính đường chéo hình lập phương. Mỗi bài tập sẽ có cách làm và trình bày khác nhau nên khi giải bài tập bạn cần chú ý. Dưới đây là những dạng bài tập tính đường chéo hình lập phương điển hình:
Bài toán 1: Cho một hình lập phương ABCD với độ dài các cạnh bằng nhau và bằng 7cm. hãy tìm đường chéo của hình lập phương đã cho.
Bài giải: Áp dụng công thức tìm đường chéo hình lập phương ta có D = a√3
=> D = 7√3
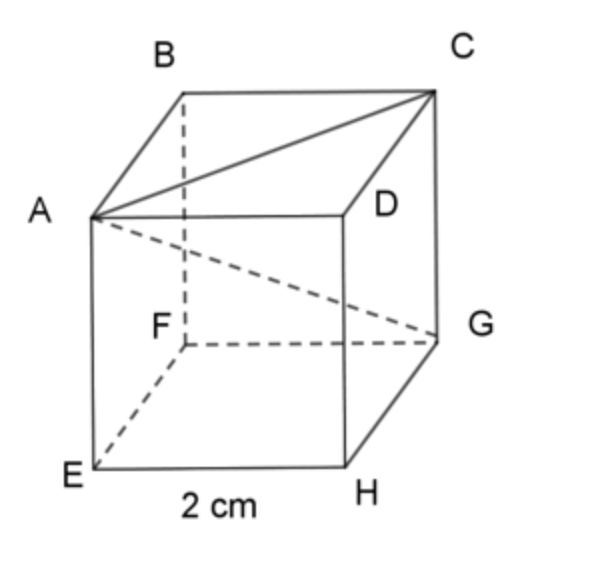
Bài toán 2: Cho một hình lập phương có cạnh a = 2cm. Hỏi độ dài đường chéo của hình lập phương bằng bao nhiêu?
Bài giải:
Theo như ký hiệu trên hình vẽ có AC là đường chéo hình vuông ABCD, AG là đường chéo hình lập phương,
Xét tam giác ABC vuông tại B:
AB2 + BC2 = AC2
⇔ 22 + 22= AC
⇔ 8 = AC2
=> AC= 2√2 (cm)
Vì ABCD.EFGH là hình lập phương nên CG sẽ vuông góc với mp (ABCD)
=> CG vuông góc với AC
Xét tam giác ACG ta có:
Ac2 + CG2 = AG2
⇔ (2√2)2 + 22= AG2
⇔ 12 = AG2
=> AG= 2√3 (cm)
Một số bài tập tìm độ dài đường chéo hình lập phương
Bài tập 1: Cho hình lập phương A có Stp là 385cm2 , hỏi thể tích hình lập phương sẽ là bao nhiêu?
- Diện tích một mặt của hình lập phương là:
384 : 6 = 64 cm2
- Độ dài cạnh của hình lập phương đó là:
64 : 8 = 8 cm
=> Thể tích hình lập phương A là: 8 x 8 x 8 = 5126 cm3
Bài tập 2: Cho hình lập phương ABCDEF có độ dài các cạnh bằng nhau, biết thể tích hình lập phương là 125cm3. Hãy tính độ dài các cạnh của hình lập phương/
Gọi a là độ dài của các cạnh hình lập phương
Thể tích của hình lập phương là: V = 125cm3
Ta áp dụng công thức tìm độ dài hình lập phương cạnh bên khi biết thể tích
a = 3
=> a = 3
=> a = 5 cm
=> Chiều dài của các cạnh hình lập phương ABCDEF là 5cm.
Bài toán 3: Hình lập phương A có canh a = 4 cm. Hình lập phương B có cạnh a gấp 2 lần cạnh hình A. Hỏi thể tích hình lập phương C gấp bao nhiêu lần so với hình lập phương A.
Bài giải:
Cạnh hình lập phương C là:
4 × 2 = 8 (cm)
Thể tích hình lập phương C là:
8 × 8 × 8 = 512 (cm³)
Thể tích hình lập phương A là:
4 × 4 × 4 = 64 (cm³)
=> 512 ÷ 64 = 8.
Vậy : Thể tích hình lập phương C gấp 8 lần thể tích của hình lập phương A.
Trên đây là một số những kiến thức liên quan đến dạng toán về đường chéo hình lập phương. Hy vọng qua bài viết này sẽ giúp phụ huynh cũng như học sinh nắm được công thức tính đường chéo hình lập phương để áp dụng vào bài tập một cách nhanh nhất, hiệu quả nhất. Bạn cần giải đáp thắc mắc về nội dung, cách tính đường chéo hình lập phương như thế nào thì hãy liên hệ ngay với Clevai để được giải đáp ngay nhé!
Nếu bạn biết một số dạng bài tính đường chéo hình lập phương nào hãy chia sẻ với Clevai ngay nhé!